Einfache Epidemie-Modelle

Ich habe mich einen Monat lang nicht gemeldet. Mir waren Zweifel gekommen, ob ich hier nicht falsche Zahlen in die Welt setzte. Ich wollte erst abklären, warum meine Rt-Werte systematisch von denen des RKI abwichen. Ich habe dabei eine Berechnungsmethode entwickelt, die eine vereinfachte Fassung der RKI-Methode ist.

Ich habe meine Überlegungen in einen Bericht geschrieben, den Sie hier downloaden können bericht.pdf (pdf, 347 KB) .
Ich würde jetzt dieses neue Verfahren bevorzugen.
Hier ist noch einmal ein aktuelles Ergebnis:

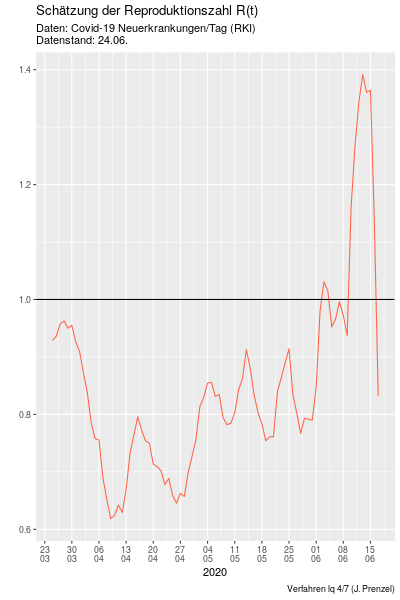
Man erkennt einen Infektions-Ausbruch in der 2. Juniwoche.
Ich würde einen Rt von 1,2 für gefährlich halten, wenn er über Wochen anhalten würde. Das scheint gerade nicht derFall zu sein. Hoffentlich bleibt es dabei.

Das Verfahren mit Namen lq 4/7 ist leicht duchzuführen, wenn man die an das RKI gemeldeten Fallzahlen hat. Der Programmier- und Rechen-Aufwandt ist, geschätzt, nur 1%
im Vergleich zu dem früher hier besprochenen Verfahren.

Ich demonstriere die Anwendung durch einen kleinen File für die für die R-Sprache: rt.r (r, 1 KB)

Damit möchte ich mich von hier verabschieden.
Bleiben Sie gesund!

Bemerkung

Das Verfahren wurde auf das sogenannte Referenzdatum des RKI umgestellt. Details sind hier beschrieben.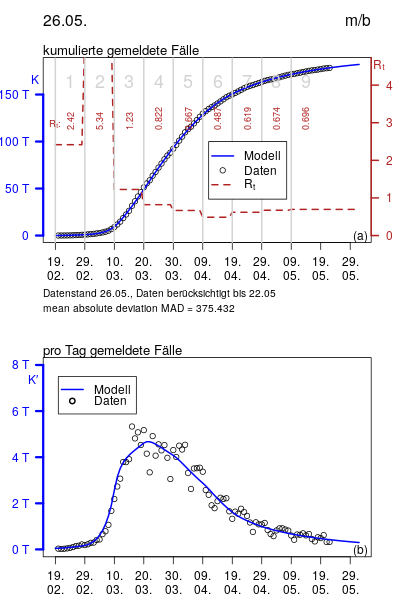

Einführung

Grundlage sind die täglich aktualisierten Fallzahlen der gegenwärtigen Covid-19 Epidemie in Deutschland. Ziel ist die Bestimmung der Reproduktionszahl Rₜ, als Funktion der Zeit.

Mit Rₜ meine ich die Anzahl der Neuinfektionen, die von einem Erkrankten in der Anfangsphase der Epidemie ausgeht. Rₜ wird durch Verhinderung von Kontakten (Lockdown) beeinflusst.

Es wird ein Modell des Typs SIR bzw SEIR verwendet. Das Modell m/b
Wird seit 16.5.2020 verwendet. Die Zeit t wird in 10 Tage breite Intervalle eingeteilt, für die jeweils ein Rₜ gesucht wird. Eine Optimierungs-Software sucht jeweils für die letzten drei Intervalle Rₜ-Werte sodass die Abweichung von den der Zeitreihe der gemeldeten Fallzahlen minimiert wird.

Ergebnis

Die Abbildung zeigt als eigentliches Ergebnis die Rₜ-Werte, die verwendet wurden, um die sichtliche Übereinstimmung zwischen dem optimalen Modelllauf und den Daten zu erzeugen. Wegen dieser Übereinstimmung wird behauptet, dass die Folge der Rₜ plausibel ist.

Das Verfahren ist so angelegt, dass eine konsistente Kette von Rₜ-Werten entsteht. Am aktuellen Ende ist die Aussage besonders unsicher, weil zukünftige Daten noch einen Einfluss haben werden.

Das neue Verfahren, das seit 22. Mai Standard ist,
wurde ein paar Tage zurück auf die am jeweilgen Tag aktuellen Daten angewandt. Es zeigt sich, dass im Verlauf der Zeit leicht unterschiedliche Rₜ geschätzt werden.

	Datenstand vom
ab	20.05.	21.05.	22.05.	23.05.	24.05.
19.2.	2.33	2.58	2.42	2.51	2.30
29.2.	5.51	5.06	5.28	5.17	5.57
10.3.	1.19	1.26	1.29	1.25	1.19
20.3.	0.84	0.82	0.80	0.81	0.83
30.3.	0.65	0.64	0.66	0.67	0.68
9.4.	0.51	0.53	0.50	0.48	0.46
19.4.	0.61	0.58	0.62	0.64	0.65
29.4.	0.64	0.68	0.64	0.64	0.63
9.5.	0.52	0.45	0.56	0.60	0.69

In der Tabelle is links das Zeitintervall angegeben, für das die Werte gelten sollen und dann nach rechts die Schätzungen anhand unterschiedlicher Datensätze. Eine gewisse Variabilität zeigen alle Werte, selbst für den März.

Das liegt wahrscheinlich daran, dass die Datensätze auch für März und April noch ziemlich in Bewegung sind. Es könnte sich darum handeln, dass noch nach vielen Wochen der Beginn einer Erkrankung in den Meldedaten nachgetragen wird.

Ich habe jetzt den Eindruck, dass für die letzten 6 Wochen ein konstanter Rₜ von 0,6 das Geschehen gut zusammenfassen würde. Kein Grund zur Aufregung von hier aus.

Seit einiger Zeit veröffentlicht das Robert-Koch-Institut zu den gemeldeten Erkrankungen ein sogenanntes Referenzdatum, das soll das Datum des Beginns der Erkrankung sein, wenn das nicht vorliegt, wird das Meldedatum als Ersatz eingetragen. Das Referenzdatum liegt im Schnitt 5 Tage vor dem Meldedatum. Die Zeitreihe der Neuerkrankungen nach Referenzdatum ist glatter und weniger vom Wochenrhythmus geprägt (s. "dashboard" des RKI).

Deshalb ist diese Datenreihe vielleicht besser geeignet, stabile Rₜ-Werte zu schätzen.

Ich will das ab heute ausprobieren, gleichzeitig will ich das Modell 10 Tage früher starten lasse, also am 20. Februar. Dazu habe ich den Startwert für die Infizierten bei t=0 auf 790 gesetzt, er war vorher bei 1500. Das geschah durch Probieren verschiedener Werte und Auswahl nach der besten Anpassung an die Daten vom 20. Feb. bis 20. März.

Es bleibt bei dem Verfahren, jeweils 3 Rₜ für drei benachbarte Intervalle von dem automatischen Optimierung bestimmen lassen, den linken der drei Werte festschreiben, das Zeitfenster um 10 Tage nach rechts verschieben usw.

Den Unterschied zwischen dem alten und dem neuen Verfahren demonstriert die Abbildung

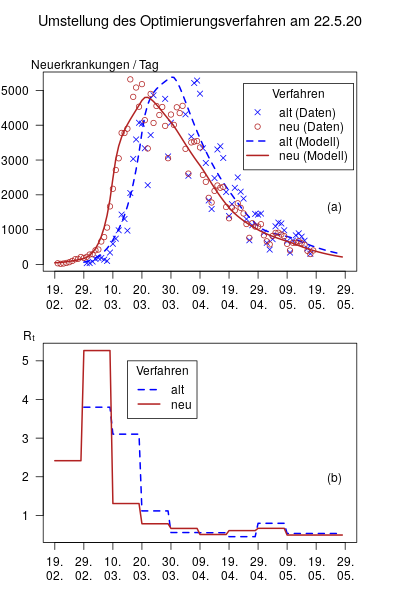
Man sieht in (a), dass die Beobachtungen sich systematisch unterscheiden. Der Erkrankungstermin liegt im Schnitt 5 Tage vor dem Meldetermin. Zusätzlich hat die Kurve eine erkennbar andere Form. Entsprechend unterscheiden sich die optimierten Rₜ-Werte (b). Der hohe Wert von ca. 5 im 2. Intervall liegt an einem früheren und steileren Anstieg in den Daten. Im april und Mai unterscheiden sich die beiden Verfahren nicht wesentlich.

Ich werde in diesem Blog bis auf weiteres die Ergebnisse des neuen Verfahrens präsentieren.

Ab und zu hört man, die Anzahl an Covid-19 Erkrankten sei viel höher als angenommen. Das wäre darauf zurückzuführen, dass viele Erkrankungen symptomlos verliefen oder als normale Erkältung abgetan würden. Man sagt, es gäbe eine hohe Dunkelziffer.

Ob das so ist, kann man man mit dem Modell m/b nicht herausbekommen. Man kann aber hypothetisch eine höhere Dunkelziffer annehmen und sehen, welchen Unterschied das macht.

Der Modellparameter q gibt an welchen Anteil an Erkrankungen das Gesundheitssystem erfasst. Ich habe hier meistens 80% angenommen. Man kann auch annehmen, dass es nur 10% sind. Ich zeige hier Ergebnisse mit q=0,1.

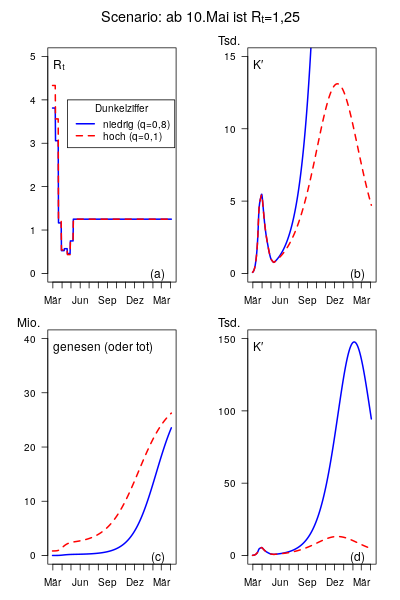
Ich habe Rₜ - Werte gefunden durch Anpassung an die Daten des RKI. Das ist möglich. Allerdings musste ich den Startwert der Erkrankungen zur Zeit Null (1.März) heraufsetzen. 14000 habe ich hier angenommen statt 1500 sonst. Es scheint plausibel, dass sich von Beginn an schon mehr Infizierte im Land befanden, wenn viele nicht als ernstlich krank auffielen. Außerdem habe ich angenommen, dass am 1. März schon 1% der Bevölkerung immun waren.

Abb. (a) zeigt dass bis 10. Mai sehr ähnliche Rₜ - Werte herausgekommen sind. Ab 10. Mai wurde, als Senario, Rₜ=1,25 angenommen. Die beiden Kurven in (b) sind bis zum 10 identisch. Das bedeutet: Mit beiden Modellvarianten ist eine Anpassung an die Daten möglich, bei fast gleichen Rₜ.

Ganz gleich sind die Modellergebnisse aber doch nicht. Das weitgehend unerkannte Krankheitsgeschehen bei q=0,1 führt früher zu einem merklichen Immunisierung in der Bevölkerung. Siehe (c).

Im Fall q=0,8 führt der angenommene Rₜ=1,25 zu einer Welle von Erkrankungen, die bis zu 150.000 Neuerkrankungen reicht (d). Im Fall q=0,1 ist die Welle viel schwächer ausgebildet.

Es wäre also gut, wenn eine hohe Dunkelziffer existierte. Nur weiß anscheinend bisher niemand, ob dem so ist.

Es geht um das Verfahren, das Werte für Rₜ sucht, die an die Daten angepasst sind. Ich stelle ein Skript für die Programmierumgebung R zur Verfügung. Das Skript optir (R, 8 KB) hat 180 Zeilen und ist mit vielen Kommentaren versehen.

Wenn man R und den Modul FME installiert hat, kann man das Skript fast sofort ausführen. Zuvor muss man noch die Daten als csv-File vom RKI besorgen und den Filenamen in den ersten Zeilen des Skripts anpassen.

Wenn jemand keine Erfahrung mit R hat, wird er das Skript wahrscheinlich nicht verstehen. Im Netz gibt es Tutorials.

Einiges sollte ich vielleicht erläutern. Das Skript ist in drei Teile geteilt.

• Die Arbeit des ersten Teils, die Daten zu lesen und umzuformen, könnte man auch ohne R erledigen.
• Im zweiten Teil werden Funktionen definiert:
  • modFit und ode stammen aus dem Modul FME
  • func ist unser Modell
  • obj stellt die Verbindung zu den Daten her
  • fitr führt die Optimierung für einen Teilabschnitt durch
• Im dritten Teil lassen wir fitr über die Zeitachse laufen. Dabei ruft fitr modFit, modFit ruft obj, obj ruft ode und ode ruft func.

Eine Kleinigkeit: ich benutze '=' anstelle des '<-', das viele Anleitungen benutzen.