Ob das so ist, kann man man mit dem Modell m/b nicht herausbekommen. Man kann aber hypothetisch eine höhere Dunkelziffer annehmen und sehen, welchen Unterschied das macht.
Der Modellparameter q gibt an welchen Anteil an Erkrankungen das Gesundheitssystem erfasst. Ich habe hier meistens 80% angenommen. Man kann auch annehmen, dass es nur 10% sind. Ich zeige hier Ergebnisse mit q=0,1.
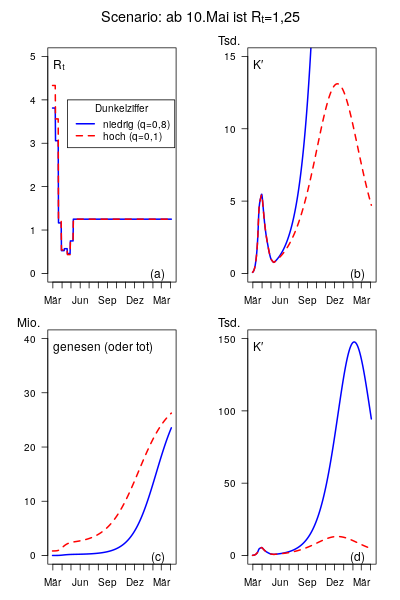
Ich habe Rₜ - Werte gefunden durch Anpassung an die Daten des RKI. Das ist möglich. Allerdings musste ich den Startwert der Erkrankungen zur Zeit Null (1.März) heraufsetzen. 14000 habe ich hier angenommen statt 1500 sonst. Es scheint plausibel, dass sich von Beginn an schon mehr Infizierte im Land befanden, wenn viele nicht als ernstlich krank auffielen. Außerdem habe ich angenommen, dass am 1. März schon 1% der Bevölkerung immun waren.
Abb. (a) zeigt dass bis 10. Mai sehr ähnliche Rₜ - Werte herausgekommen sind. Ab 10. Mai wurde, als Senario, Rₜ=1,25 angenommen. Die beiden Kurven in (b) sind bis zum 10 identisch. Das bedeutet: Mit beiden Modellvarianten ist eine Anpassung an die Daten möglich, bei fast gleichen Rₜ.
Ganz gleich sind die Modellergebnisse aber doch nicht. Das weitgehend unerkannte Krankheitsgeschehen bei q=0,1 führt früher zu einem merklichen Immunisierung in der Bevölkerung. Siehe (c).
Im Fall q=0,8 führt der angenommene Rₜ=1,25 zu einer Welle von Erkrankungen, die bis zu 150.000 Neuerkrankungen reicht (d). Im Fall q=0,1 ist die Welle viel schwächer ausgebildet.
Es wäre also gut, wenn eine hohe Dunkelziffer existierte. Nur weiß anscheinend bisher niemand, ob dem so ist.
... comment